|
10/12/2017 0 Comments Even and Odd Functions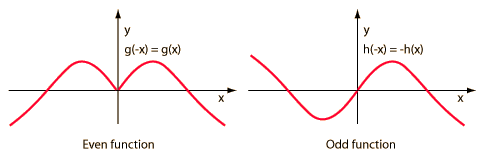 Even functions are functions in which f(x) is equal to f(-x). They have y-axis symmetry. Odd functions are functions in which f(-x) is equal to -f(x). They have origin symmetry. Both functions have a form of symmetry, but the type depends on whether the function is even or odd. You can check algebraically (does f(x) equal f(-x), f(-x) equal -f(x), or neither). You can also check graphically (y-axis symmetry, origin symmetry, or neither). Function families that are even are parabolas and lines. One that is odd is cubed root. I don't really have any questions from this assignment. It all more or less makes sense to me.
0 Comments
Leave a Reply. |
 RSS Feed
RSS Feed
